The following simplified example illustrates the basic operation of life insurance as a capital accumulation vehicle with both death protection and savings components. Suppose five people form a capital accumulation lottery pool or syndicate with the objective that each of them will receive $1,000 from the pool over a five-year period. Each person will contribute the same amount to the pool in each year that he or she still participates. However, at the end of each year, one of them, selected by lot, will be paid his or her $1,000 payout and will drop out of the pool. Only those persons remaining continue to make whatever contributions are necessary to fund for the $1,000 distributions in subsequent years. The expected or average number of years until any given participant in this pool will receive his or her payout is three years. Assuming a 10 percent rate of return, the amount any one of them would have to save at the beginning of each year for three years to accumulate $1,000 is $274.65.
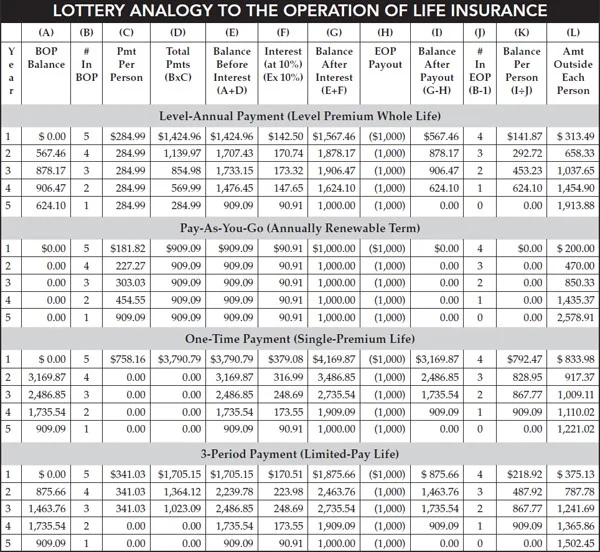
The chart above shows how much each participant would have to contribute each year to assure the necessary funds to pay $1,000 out of the pool each year to the person selected by lot using various funding or financing arrangements that are similar to typical insurance premium payment plans.
For example, in the “level-annual payment” section of the chart each participant is assumed to contribute a level $284.99 at the beginning of each year that he or she is still a participant in the pool. With these contributions, the pool will be adequately funded throughout the five-year period. Specifically, each of the five participants pays $284.99 the first year for a total of $1,424.96. With interest credited at 10 percent, the end-of-year balance before distribution of the first $1,000 lottery payout is $1,567.46. The lucky winner is selected and paid $1,000, leaving $567.46 in the pool to help fund later distributions. This works out to $141.87 for each person who remains in the pool. In the second year, each of the remaining four participants again contributes $284.99, totaling $1,139.97. This amount, together with the carryover balance from the prior year, $567.46, will grow at 10 percent to $1,878.17 by the end of the second year when the second payout occurs. After paying $1,000 to the lucky winner, $878.17, or $292.72 per remaining participant, is left in the pool. The aggregate amount in the pool first increases and then declines as participants receive their $1,000 payouts and drop out. However, the balance or “reserve” per participant continues to increase each year until the last year when the remaining balance plus the last year contribution and interest earnings thereon equal the final required payout of $1,000.
This lottery pool arrangement is a simplified description of how a level-premium life insurance plan works. If this were a level-premium life insurance plan, the probabilities used would represent the chance of any given person dying each year rather than the chance of winning the lottery.
The “premium” each participant would pay ($284.99) is very close to the amount he or she would have to save each year ($274.65) to accumulate $1,000 by the end of his or her “life expectancy,” which, in this simplified case is three years. However, just like in real life, although each participant can expect to live a certain period of additional years, in this case, three years, some will die sooner and some will die later. The pooling arrangement is a risk-sharing mechanism that assures each participant that he or she will receive $1,000 regardless of when he or she dies, just as if he or she were certain to live to life expectancy and saved virtually the same amount as the premium each year.
Those participants who die sooner may be losers in the “game of life,” but they are compensated by winning the lottery. They obviously receive more from the pool than they could have accumulated outside the pool arrangement by the time they die. For comparison, column (L) in Figure 1.2 shows how much any given participant would have accumulated by the end of each year if contributions had been invested outside the pool at the same 10 percent rate of return. For example, in the level-payment plan, the person who dies the first year and receives $1,000 would have accumulated only $313.49—or $686.51 less if the “premium” had been invested outside the plan.
The participants who die late are winners in the “game of life,” but losers in the lottery. They actually receive less than they would have accumulated outside the pool by the time they die. For example, once again looking at the level payment plan, the person who dies in year five, receiving $1,000, would have accumulated almost twice as much, $1,913.88, if premiums had been invested outside the plan. 3However, because nobody knows who will die sooner and who will die later, all participants are “winners” if their mutual objective is to assure that they will receive no less than $1,000 regardless of when they die. For essentially the same annual payment as it would take to accumulate the desired sum if they each lived to life expectancy, they eliminate the risk of under-accumulating if they should die early. And, if they happen to be one of the longer-lived participants, they are still assured they will accumulate at least the minimum desired amount of $1,000.
As is characteristic of level-premium and other cash-value life insurance, the pool builds up reserves or cash values that are necessary to cover shortfalls that arise when there are fewer participants remaining who pay into the pool in later years. These values are shown in column (K). Although the aggregate reserves or cash value balances in the pool decline in the later years [columns (E) and (G)], they continue to increase throughout the five-year payout period on a per-participant basis, which is analogous to how level premium life plans work. This per-person reserve or cash balance is the “savings” element of the arrangement and is the source for policy loans, cash surrender values, and other “living” benefits in cash-value insurance plans. If a person dropped out of the pool before dying, he or she could take his or her individual cash balance without jeopardizing the cash accumulation necessary to ultimately pay $1,000 to the remaining participants.
The second section of the chart shows a “pay-as-you-go” lottery pool that is analogous to an annually renewable term insurance plan. Similar to the level-annual payment lottery pool described above, the pool pays $1,000 at the end of each year to one participant determined by lot. Each remaining participant’s contribution each year is equal to the amount that, when aggregated and invested at 10 percent interest, is just sufficient to pay $1,000 out of the pool at the end of the year with nothing left over. In contrast with the level-annual payment lottery pool and level premium life insurance plans, there is no accumulated reserve or cash balance, which is analogous to an annually renewable term insurance plan. As this example clearly demonstrates, the pay-as-you-go annually renewable term plan starts with lower required premium payments than the level-premium plan, but they quickly increase and exceed the level-premium payments by the third year. The annually renewable term plan creates bigger economic “winners” and bigger economic “losers” than the level-premium plan. Those who die sooner, get a much greater effective return on their “investment” because their total payments into the pool are much less. Those who die later, get a much lower (negative) return on their investment because they must make much greater total payments to the pool. However, once again, all participants are “winners” under this arrangement relative to a savings plan outside the pool if their principal objective is sharing the risk to assure they each accumulate at least $1,000 regardless of when they die.
The last two sections of the chart use the lottery analogy to show how single-premium life and limited-pay life compare to level-premium life and annually renewable term plans in this simplified example. When the paying period is shortened relative to the payout period, the total contributions necessary to fund later payouts are accelerated and the annual amounts paid in must necessarily increase. However, the per-person reserves or cash balances also increase the savings component of each participant’s total investment increases while the pure death protection component decreases. Furthermore, the total amount any given participant must pay, even the longest surviving participant, declines. In other words, from an economic standpoint, there is a smaller difference in the total cost of the program between the “winners” who die early and the “losers” who die late because the contingent or pure death protection component of the total investment has decreased.
Elements of Life Insurance Premium Pricing and Cash Value Calculations
Risk Shifting and Risk Sharing
A common misconception about life insurance is that the risk of premature death is transferred to the insurance company. Although insurance companies must have a certain amount of surplus or paid-in capital to cover potential excess losses, they price their products to maintain or even increase the surplus and paid-in capital over time. Therefore, risk is shifted to or shared among all insureds in the insurance pool. Those policy owners who live a long time carry the economic burden for those who do not. However, there is less risk sharing with premium-payment plans that generate a greater “savings” component, such as single-premium life insurance, than with those that have a greater “pure death protection” component, such as annually renewable term. One can view the savings component of life insurance, similar to other investments, as a form of self-insurance, because it is available regardless of whether the insured lives or dies. If the self-insurance component is greater, the amount of risk that all participants in the pool must share among themselves is obviously less.
Premiums and Costs
Another common misconception is that higher premiums mean higher cost. The various payment plans in the chart above demonstrate the fallacy of that conception. By design, each of the premium payment plans in the chart is actuarially equivalent. In each case, the expected value of each participant’s payments is exactly equal to his or her expected return, $1,000. In principle, life insurance companies determine premiums in the same way. From an actuarial standpoint, there are no differences between one premium-payment plan and another for a given level and term of coverage because they are all priced to be equivalent on a present value or prospective basis.
The actual after-the-fact cost to the insured may vary substantially from one premium payment plan to another, as is also clearly demonstrated by the illustrated values in the chart. If a person dies soon, the pay-as-you-go term insurance plan is relatively the best economic deal. But it is also the worst deal for a person who lives a long time. Conversely, the single-premium plan is relatively the best deal if a person lives a long time, but the worst deal if death comes early. Clearly, all else being equal (which it is not because of the unique income and estate tax features as well as other characteristics of life insurance), if a person could be sure that he or she would live longer than average for his or her age, the best deal would be to invest outside of life insurance in conventional investments. But nobody can ever have that assurance.
Interest Rates
The required contribution levels (premiums) under the various payment plans in the chart illustrations were computed using an interest assumption of 10 percent and highly simplified mortality factors. Similarly, insurance companies must make assumptions about the interest they will earn on assets and the mortality experience of their pool of insureds to compute the required premiums. If the insurance company assumes that it can invest the reserves (the “savings” component) to earn high-interest rates, the required premiums will be lower. If the company assumes a lower interest rate, premiums will be higher. For most life insurance policies, life insurance companies guarantee that they will credit an interest rate to the policy owner’s “savings” components that will equal or exceed a certain minimum rate, ranging from 4 to 6 percent (except on variable life products). The maximum interest rate that an insurer may assume when computing required premiums and reserves is limited by statute.
Mortality and Morbidity and the Law of Large Numbers
Mortality refers to the number of deaths within a given time or a given community. Generally, it is expressed as a rate reflecting the proportion of deaths to population, or to a specific number of the population such as per 1,000, 10,000, or 100,000 lives. Actuaries compute mortality for various large groups of people based upon demographic factors such as sex, age, race, and country or area or residence, and other factors such as occupation, educational level, income level, and habits or hobbies (e.g., smoker versus nonsmoker). They create tables of mortality exhibiting the average relative number of persons who survive, or who have died, at the end of each year of life, out of a given number supposed to have been born at the same time.
The term morbidity is sometimes used in the same sense as mortality, but it is actually a more general term relating to the incidence of disease within a community, including both fatal and nonfatal cases.
Insurance companies base their mortality assumptions on the experience of large groups of people. By the law of large numbers, actuaries can estimate the proportion of a large group of people with similar characteristics of a given age who will die within a given year with remarkable accuracy. Technically, the law of large numbers says that in repeated, independent trials with the same probability “p” of success in each trial, the chance that the percentage of successes differs from the probability “p” by more than a fixed positive amount “e > 0” converges to zero as the number of trials “n” goes to infinity, for every positive “e.” In other words, as the number of people of the same age and with similar characteristics increases, the rate of actual deaths experienced by the group will get closer and closer to the expected rate of deaths for the group at any given age.
Reproduced with permission. Copyright The National Underwriter Co. Division of ALM


